计算方式 计算方式有哪几种

计算方式又称“数值分析”。是为各种数学问题的数值解答研究提供最有效的算法。主要内容为函数逼近论，数值微分，数值积分，误差分析等。常用方法有迭代法、差分法、插值法、有限元素法等。

文章目录：

1. 计算方式
2. 加减乘除的计算方法
3. 15种巧算方法

一、计算方式

计算方式又称“数值分析”。是为各种数学问题的数值解答研究提供最有效的算法。

主要内容为敏兆函数逼近论，数值微分，数值积分，误差分析等。

常用方法有迭代法、差分法、插值法、有限元素法等。现代的计算方法还要求适应电子计算机的特点。数值分析即“答配计清拿指算方式”。

二、加减乘除的计算方法

先乘除,后加减,有括号的先算括号里的.

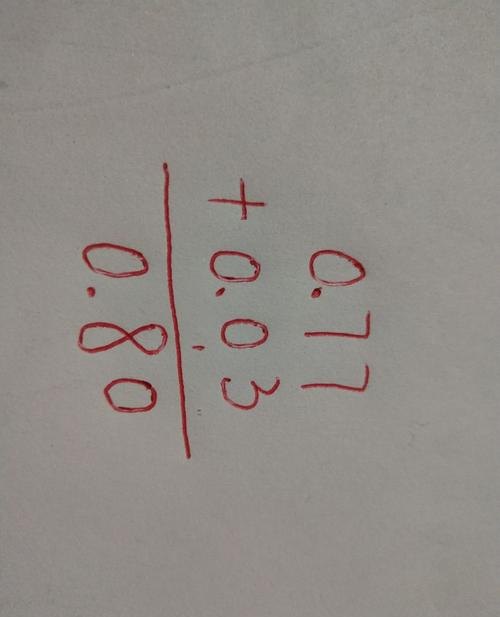
整数加、减计算法则：

1）要把相同数位对齐，再把相同计数单位上的数相加或相减；

2）哪一位满十就向前一位进。

2、小数加、减法的计算法则：

1）计算小数加、减笑搏改法，先把各数的小数点对齐（也就是把相同数位上的数对齐），

2）再按照整数加、减法的法则进行计算，最后在得数里对齐横线上的小数点点上小数点。

（得数的小数部分末尾有0，一般要把0去掉。）

3、分数加、减计算法则：

1）分母相同时，只把分子相加、减，分母不变；

2）分母不相同时，要先通分成同分母分数再相加、减。

4、整数乘法法则：

1）从右起，依次用第二个因数每位上的数去乘第一个因数，乘到哪一位，得数的末尾就和第二个因数的哪一位对个因数的哪一位对齐；

2）然后把几次乘得的数加起来。

（整数末尾有0的乘法：可以先把0前面的数相乘，然后看各因数的末尾一共有几个0，就在乘得的数的末尾添写几个0。）

5、小数乘法法则：

1）按整数乘法的法则算出积；

2）再看因数中一共有几位小数，就从得数的右边起数出几位，点上小数点。

3）得数的小数部分末尾有0，一般要把0去掉。

6、分数乘法法则：把各个分数的分子乘起来作为分子，各个分数的分母相乘起来作为分母，（即乘上这个分数的倒数），然后再约分。

7、整数的除法法则

1）从被除数的商位起，先看除数有几位，再用除数试除被除数碰判的前几银孝位，如果它比除数小，再试除多一位数；

2）除到被除数的哪一位，就在那一位上面写上商；

3）每次除后余下的数必须比除数小。

8、除数是整数的小数除法法则：

1）按照整数除法的法则去除，商的小数点要和被除数的小数点对齐；

2）如果除到被除数的末尾仍有余数，就在余数后面补零，再继续除。

9、除数是小数的小数除法法则：

1）先看除数中有几位小数，就把被除数的小数点向右移动几位，数位不够的用零补足；

2）然后按照除数是整数的小数除法来除

10、分数的除法法则：

1）用被除数的分子与除数的分母相乘作为分子；

2）用被除数的分母与除数的分子相乘作为分母

三、15种巧算方法

1.方法1.两位数加两位数的进位加法。 口诀： 加9要减1，加8要减2，加7要减3，加6要减4，加5要减5，加4要减6，加3要减7，判伏燃巧加2要减8，加1要减9。 （注： 口决中的加几都是说个位上的数）。2.方法2.两位数减两位数的退位减法。 口决： 减9要加1，减8要加2，减7要加3，减6要加4，减5要加5，减4要掘段携加6，减3要加7，减2要加8，减1要加9。

凑整巧算”——运用加法的交换律、结合律进行计算。

运森行用乘法的交换律、结合律进行简算。

运用减法的性质进行简算，同时注意逆进行。

运用除法的性质进行简算 (除以一个数，先化为乘基春岩以一个数的倒数，再分配)。

运用乘法分配律进行简算。

混合运算（根搏御据混合运算的法则）。

具体解释：

一、“凑整巧算”——运用加法的交换律、结合律进行计算。

凑整，特别是“凑十”、“凑百”、“凑千”等，是加减法速算的重要方法。

加法交换律

定义：两个数交换位置和不变，

公式：A+B =B+A，

例如：6+18+4=6+4+18

加法结合律

定义：先把前两个数相加，或者先把后两个数相加，和不变。

公式：（A+B）+C=A+(B+C)，

例如：(6+18)+2=6+(18+2)

引申——凑整

例如：1.999+19.99+199.9+1999

=2+20+200+2000-0.001-0.01-0.1-1

=2222-1.111

=2220.889

二、运用乘法的交换律、结合律进行简算。

乘法交换律

定义：两个因数交换位置，积不变.

公式：A×B=B×A

例如：125×12×8=125×8×12

乘法结合律

定义：先乘前两个因数，或者先乘后两个因数，积不变。

公式：A×B×C=A×(B×C),

例如：30×25×4=30×（25×4）

三、运用减法的性质进行简算，同时注意逆进行。

减法

定义：一个数连续减去两个数，可以先把后两个数相加，再相减。

公式：A－B－C=A－(B+C)，【注意：A－(B+C)= A－B－C的运用】

例如：20－8－2=20－（8+2）

四、运用除法的性质进行简算 (除以一个数，先化为乘以一个数的倒数，再分配)。

除法

定义：一个数连续除去两个数 ，可以先把后两个数相乘，再相除。

公式：A÷B÷C=A÷(B×C)，

例如：20÷8÷1.25=20÷(8×1.25)

定义：除数除以被除数，把被除数拆为两个数字连除（这两个数的积一定是这个被除数）

例如：64 ÷16=64÷8÷2=8÷2=4

五、运用乘法分配律进行简算。

乘法分配律

定义：两个数的和与一个数相乘，可以先把它们与这个数分别相乘，再相加。

公式：（A+B）×C=A×C+B×C

例如;2.5×(100+0.4)= 2.5×100+2.5×0.4= 250+1= 251

六、混合运算（根据混合运算的法则）。

学会数字搭配（ 0.5和2、0.25和4、0.125和8）

以上内容由火焰鸟网站（dk.hynjr.com）小编收集整理于互联网，目的在于传递更多信息，并不代表本网赞同其观点。其内容真实性、完整性不作任何保证或承诺。如若本网有任何内容侵犯您的权益，请及时联系我们，本站将会在24小时内处理完毕。